For which value of p the series converges?
Therefore, for the series to converge conditionally, we need p < 1, so that the absolute value of each term decreases monotonically and approaches 0 as k approaches infinity. For the series to diverge, the absolute value of at least one term must not approach 0 as k approaches infinity.
For what value of p is convergent?
With p-series, if p > 1, the series will converge, or in other words, the series will add up to a specific numerical value.
Which P-series are convergent?
In general, a p-series follows the following form: is convergent if p > 1 and divergent otherwise.
Do P-series converge to 0?
They are convergent when and divergent when 0 < p ≤ 1 .
For what values of p does the series below converge?
Expert-Verified Answer In a p-series, the series converges for values of p greater than 1, and diverges for values of p less than or equal to 1.
What is the value of convergent series?
The sum of a convergent geometric series can be calculated with the formula a⁄1 – r, where “a” is the first term in the series and “r” is the number getting raised to a power. A geometric series converges if the r-value (i.e. the number getting raised to a power) is between -1 and 1.
Do alternating P-series always converge?
Given an alternating series , ∑ ( − 1 ) k a k , if the sequence of positive terms decreases to 0 as , k → ∞ , then the alternating series converges. Note that if the limit of the sequence is not 0, then the alternating series diverges.
How do we know if a series is convergent?
If a series is a p-series, with terms 1np, we know it converges if p>1 and diverges otherwise. If a series is a geometric series, with terms arn, we know it converges if |r|<1 and diverges otherwise. In addition, if it converges and the series starts with n=0 we know its value is a1−r.
Why is a series convergent?
Convergence and divergence If the sum of a series gets closer and closer to a certain value as we increase the number of terms in the sum, we say that the series converges. In other words, there is a limit to the sum of a converging series. If a series does not converge, we say that it diverges.
Which of the series is convergent?
If r < 1, then the series is absolutely convergent. If r > 1, then the series diverges. If r = 1, the ratio test is inconclusive, and the series may converge or diverge. where “lim sup” denotes the limit superior (possibly ∞; if the limit exists it is the same value).
Do series only converge to 0?
If the series converges, that means that a sum of infinitely many numbers is equal to a finite number! If the sequence {an} diverges or converges to anything other than 0, then the series ∑an diverges. If the sequence {an} converges to 0, then the series ∑an may converge or may diverge.
Can a positive sequence converge to 0?
As the number of terms in the sequence approaches infinity, the value of the terms approaches zero. Thus, the sequence converges to zero. Consider the sequence {1, 2, 4, 8, 16, …}.
What makes a limit convergent?
Remember that a sequence is convergent if its limit exists as n → ∞ n\to\infty n→∞. So it makes sense that once we know that a sequence is convergent, we should be able to evaluate the limit as n → ∞ n\to\infty n→∞ and get a real-number answer.
For what values of is the series conditionally convergent?
To summarize, the convergence properties of the alternating p-series are as follows. If p > 1, then the series converges absolutely. If 0 < p ≤ 1, then the series converges conditionally. If p ≤ 0, then the series diverges.
When to use p-series test?
Use the p-series test to say whether or not the series converges. In this format, we can see that p = 1 / 2 p=1/2 p=1/2. The p-series test tells us that a n a_n an diverges when p ≤ 1 p\le1 p≤1, so we can say that this series diverges. Let’s try a second example.
How do you prove a series converges?
The geometric series ∑ an converges if |a| < 1 and in that case an → 0 as n → ∞. If |a| ≥ 1, then an → 0 as n → ∞, which implies that the series diverges. The condition that the terms of a series approach zero is not, however, sufficient to imply convergence.
How do you prove P-series converges?
If it’s a p-series ∑ 1 np , you know if it converges or not. It converges when p > 1. If the terms don’t approach 0, you know it diverges. If you can dominate a known divergent series with the series, it diverges.
For what value of p does the integral converge?
For x−p, if p<1, the integral converges because the function x−p does not become infinitely large as x approaches 0. Conversely, if p≥1, the function becomes infinitely large as x approaches 0, causing the integral to diverge.
For what values of p will both series and converge responses?
Expert-Verified Answer The p-series ∑k=1 to ∞ (1/k^p) converges if and only if p > 1, and diverges for p ≤ 1.
How do you identify a convergent series?
When the limit of a series approaches a real number (i.e., the limit exists), it displays convergent behavior. As a result, an approximation can be evaluated for that given series. However, if the limit does not exist or is equal to infinity, that series displays divergent behavior.
Why the series is convergent?
A series converges if the partial sums get arbitrarily close to a particular value. This value is known as the sum of the series.
What are the characteristics of a convergent series?
A series in which the sum of the series tends to a definite value as the number of terms tends to infinity is called a convergent series. As k tends to infinity then n tends to infinity and so the sum tends to infinity. The sum of an infinite arithmetic series is infinity.
How to determine if a series is absolutely convergent or conditionally convergent?
In other words, a series converges absolutely if it converges when you remove the alternating part, and conditionally if it diverges after you remove the alternating part.
Is AP series always convergent?
As with geometric series, a simple rule exists for determining whether a p-series is convergent or divergent. A p-series converges when p > 1 and diverges when p < 1.
What value does an alternating series converge to?
In other words, if the absolute values of the terms of an alternating series are non-increasing and converge to zero, the series converges. This is easy to test; we like alternating series.
What are all values of p for which the infinite series converges responses?
Therefore, the infinite series converges when p > 1, and diverges when p is in the interval (0,1).
Does the series converge faster for P 2 or P 3 explain?
The series converges faster for p = 3 because the denominator of the expression gets larger faster.
For what values of p will both series and converge responses?
Expert-Verified Answer The p-series ∑k=1 to ∞ (1/k^p) converges if and only if p > 1, and diverges for p ≤ 1.
What value does a power series converge to?
Since the terms in a power series involve a variable x, the series may converge for certain values of x and diverge for other values of x. For a power series centered at x=a, the value of the series at x=a is given by c0. Therefore, a power series always converges at its center.
Are P series convergent or divergent?
How do you know if a series is convergent?
What is a convergent series test?
Which series is convergent According to the ratio test?
Alright, let’s dive into this! You’re asking about a pretty important concept in calculus – convergence of series. Specifically, we’re looking at p-series, which are series of the form 1/n^p, where *n* is a positive integer and *p* is a real number.
Now, the big question is: for what values of *p* does this series converge?
Let’s break it down:
What does convergence mean?
Imagine a series like 1 + 1/2 + 1/4 + 1/8 + …. As you add more terms, the sum gets closer and closer to a specific value. In this case, the sum approaches 2. We call this convergence.
What if it doesn’t converge?
If the sum of the series keeps getting bigger and bigger without reaching a specific value, we say the series diverges.
So, how do we determine convergence for p-series?
There’s a handy rule for p-series. It’s like a magic formula:
The p-series 1/n^p converges if *p* > 1 and diverges if *p* ≤ 1.
Let me break it down further:
If *p* is greater than 1: Think of it this way – the terms in the series are getting smaller and smaller really quickly. This allows the series to approach a finite value, so it converges.
If *p* is less than or equal to 1: The terms in the series don’t decrease fast enough. They can still add up to infinity, causing the series to diverge.
Let’s look at some examples:
p = 2: The series 1 + 1/4 + 1/9 + 1/16 + … converges because *p* > 1.
p = 1: The series 1 + 1/2 + 1/3 + 1/4 + … diverges because *p* ≤ 1.
Want to test your knowledge?
Let’s try one:
Is the series 1 + 1/√2 + 1/√3 + 1/√4 + … convergent or divergent?
Think about it. √2, √3, √4 are all greater than 1. So, p would be less than 1. Therefore, this series is divergent.
Why is this important?
Understanding convergence is crucial in many areas of math, especially when dealing with functions, integrals, and differential equations. It helps us determine if a particular function or solution is valid or behaves in a predictable way.
FAQs
Q: What are some other types of series besides p-series?
A: There are many! Some examples include:
Geometric series: These have a common ratio between terms.
Alternating series: These have alternating signs (+ and -) between terms.
Power series: These are series where each term is a power of a variable.
Q: How do I determine convergence for other types of series?
A: There are various tests you can use, such as:
The ratio test
The integral test
The comparison test
Q: Are there any online tools that can help me determine convergence?
A: Yes, there are! Search for “series convergence calculator” online. These tools can help you test different series and understand the convergence criteria.
Remember, understanding convergence is key to understanding the behavior of infinite series. And, with practice and a little exploration, you can master this concept!
See more here: For What Value Of P Is Convergent? | For What Values Of P Is The Series Convergent
For what values of p is given series convergent.
I tried to check values of $p$ for which series is absolutely convergent and using integral test I think it will work for $p<-1$. Using alternating series test, I think $p$ can take all negative real values and $0$ also. Mathematics Stack Exchange
Convergent series – Definition, Tests, and Examples
A convergent series exhibit a property where an infinite series approaches a limit as the number of terms increase. This means that given an infinite series, ∑ n = 1 ∞ a n = a 1 + a 2 + a 3 +, the series is said The Story of Mathematics
Proof of p-series convergence criteria (article) | Khan Academy
p -series have the general form ∑ n = 1 ∞ 1 n p where p is any positive real number. They are convergent when p > 1 and divergent when 0 < p ≤ 1 . The AP Calculus course Khan Academy
How can I find for which values of $p$ this series converges?
The series is $\sum_{k=2}^\infty\frac{1}{k(\ln(k))^p}$. I know $\sum_{k=2}^\infty\frac{1}{k(\ln(k))}$ diverges but don’t know how to go about finding Mathematics Stack Exchange
Calculus II – Convergence/Divergence of Series – Pauls Online
The sequence of partial sums is convergent and so the series will also be convergent. The value of the series is, \[\sum\limits_{n = 1}^\infty {\frac{1}{{{3^{n – 1}}}}} Pauls Online Math Notes
Series Convergence Calculator – Symbolab
Free series convergence calculator – Check convergence of infinite series step-by-step Symbolab
Find values of $p$ for which the series is convergent.
$\frac{1}{2}\int_{u=2}^{\infty}u^pdu$ is known to converge $\forall p<-1$, thus the series you provided will converge for all $p<-1$. Mathematics Stack Exchange
The p-Series and Estimating Series Value | Calculus II – Lumen
Definition. For any real number p p, the series. ∞ ∑ n=1 1 np ∑ n = 1 ∞ 1 n p. is called a p-series. We know the p -series converges if p = 2 p = 2 and diverges if p =1 p = 1. Lumen Learning
Worked example: p-series (video) | Khan Academy
Now you might immediately recognize this as a p-series, and a p-series has the general form of the sum, going from n equals one to infinity, of one over n to the p, Khan Academy
8.2: Convergence of Power Series – Mathematics LibreTexts
Consider the power series \[f(z) = \sum_{n = 0}^{\infty} a_n (z – z_0)^n. \nonumber \] There is a number \(R \ge 0\) such that: If \(R > 0\) then the series converges absolutely to an Mathematics LibreTexts
See more new information: charoenmotorcycles.com
Find The Values Of P For Which The Series Converges. {1/(N(Ln N)^P)}. Integral Test
For Which Values Of P Will The Series Converge?
Find The Values Of P Which The Series Is Convergent. {Ln N/(N^P)}. Integral Test
The P-Integral Proof (Type 1 Improper Integral)
Series Of N(1+N^2)^P, Sect11.3#31
Choosing Which Convergence Test To Apply To 8 Series
Find P For Which The Series Converges Sum((-1)^N(1/N^P))
5.10 Example 4 For What Values Of P Is The Integral Convergent?
Calculus Help: Find The Values Of P For Which The Integral Converges. 1/X(Lnx)^P
Link to this article: for what values of p is the series convergent.
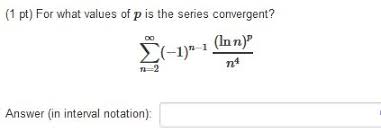
See more articles in the same category here: https://charoenmotorcycles.com/how